Figure 4 - Vista del modello dall’alto con le sezioni A-B e C-D
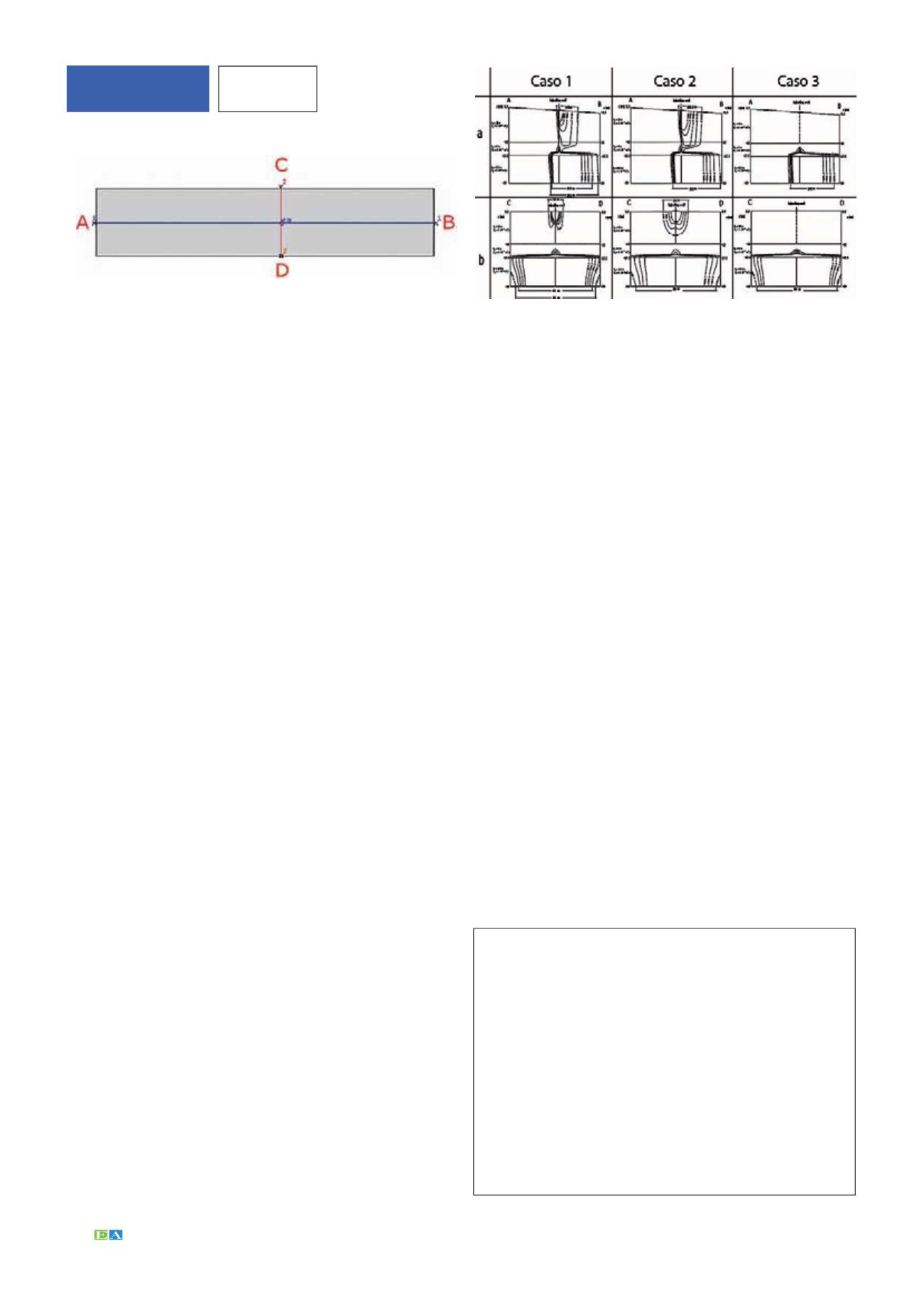
Figura 5 - Gli effetti della ricarica differenziale in un acquifero a due strati con
diverse trasmissività. Tra gli acquiferi, si trova un sottile aquiclude. Le simulazioni
dimostrano la possibilità di generare variazioni di grandi estensioni di acqua
dolce iniettata in acquiferi salati, utilizzando diversi tassi di Áusso negli acquiferi
28
n.15 settembre 2014
ACQUA
GESTIONE
Risultati delle simulazioni
La letteratura scienti¿ca dimostra che l’intrusione di acqua salata
può essere evitata iniettando acqua dolce in pozzi disposti in serie.
In questo studio sono stati simulati gli effetti dell’iniezione di acqua
dolce per mezzo di un modello descritto preventivamente, con lo
scopo di sottolineare che la fornitura di un diverso tasso d’afÀusso
nei pozzi, secondo le variazioni di permeabilità, può migliorare gli
effetti dell’iniezione. Per questo motivo sono state effettuate due
simulazioni:
- l’acqua dolce è stata iniettata per mezzo di due pozzi, sia aven-
do le aperture nell’acquifero più trasmissivo, l’altro in quello meno
trasmissivo; il tasso di Àusso dei due pozzi d’iniezione è lo stesso;
- l’acqua dolce è stata iniettata con un tasso di Àusso proporzionale
alla trasmissività dell’acquifero.
Il pozzo d’iniezione è identi¿cato con la lettera a (Figura 4) ed è po-
sizionato all’incrocio di due sezioni lungo le quali si vuole studiare il
modello. L’iniezione con lo stesso tasso causa, secondo la formula
di Dupuit, un aumento piezometrico limitato da un pro¿lo quasi pa-
rabolico. La forma della ‘zona di ricarica’ è identica alla zona di cat-
tura di un pozzo di pompaggio. Il rapporto della larghezza del fronte
dei due pozzi è l’inverso del rapporto tra le trasmissività. Gli stessi
risultati sono ottenuti dalle simulazioni, iniettando acqua fresca in
un pozzo che ha le aperture localizzate in entrambi gli acquiferi con
diverse trasmissività. Si è dedotto che negli acquiferi strati¿cati con
diverse trasmissività, spesso la ricarica non può evitare l’intrusione
di acqua salata, dove la trasmissività è maggiore. Iniezione di un
tasso di Àusso proporzionale alle trasmissività, genera una “zona
di ricarica” della stessa forma e larghezza. In queste condizioni,
le simulazioni dimostrano che l’occorrenza dell’intrusione di acqua
salata negli strati nelle sezioni di acquifero più permeabili sparisce.
Per questo motivo, la ricarica differenziale, cioè l’utilizzo di tassi di
Àusso di acqua dolce proporzionali alle trasmissività a diverse pro-
fondità, può essere una buona soluzione in molti casi di acquiferi
verticalmente eterogenei.
Discussione dei risultati
Le simulazioni avvalorano le ipotesi che la ricarica differenziale
possa avere buoni effetti sulla conservazione della potabilità del-
le acque lungo le coste, evitando l’intrusione di acqua salata nel-
le parti più permeabili dell’acquifero. Per poter valutare l’ef¿cacia
dell’intervento, è necessario porre a confronto, tramite un modello
matematico, l’estensione e il volume della porzione di acquifero che
la barriera di ricarica può saturare di acqua dolce, variando il livello
acquifero in cui avviene la ricarica e la portata iniettata. Per avere
buoni risultati, dato che gli acquiferi in generale sono strati¿cati, con
livelli a permeabilità diversa, è indispensabile una ricostruzione ac-
curata della geologia dell’acquifero e della distribuzione delle per-
meabilità e delle trasmissività al suo interno. In tal modo è possibile
evidenziare attraverso una serie di simulazioni, quali sono i livelli
nei quali è più opportuno effettuare la ricarica con acqua dolce, e la
portata di acqua dolce che deve essere iniettata in ciascuno di essi.
Per il calcolo dei limiti della barriera di ricarica, sono stati presentati
metodi analitici da Shan (1999), Christ and Goltz (2004), ed è stato
sviluppato un nuovo modello per una serie di pozzi (Colombo
et
al.
, 2012, in press). Questo modello considera non solo un numero
di pozzi N2, ma anche la possibilità di posizionare i pozzi ovun-
que nel piano complesso (x, y). Al ¿ne di usare questo modello,
qualsiasi sempli¿cazione è necessaria: l’acquifero deve essere
omogeneo, isotropico, con¿nato con uno spessore uniforme B e
la velocità costante di Darcy J. Il Àusso è stazionario. Il potenziale
complesso w (Javandel and Tsang, 1984), dall’equazione lineare di
Laplace, può essere espresso come sovrapposizione degli effetti di
un sistema formato da N iniezioni o pozzi di pompaggio e acqua
sotterranea.
Per ottenere la formula della funzione della curva di cattura, c’è
bisogno innanzitutto di valutare la funzione del Àusso in un punto di
stagnazione, che corrisponde alla velocità uguale a 0.
Un altrometodo che ha fornito buoni risultati consiste nellamodella-
zione numerica della zona di ricarica per mezzo di FeÀow (Diersch,
1996). Questi metodi permettono d’identi¿care con precisione le
aree in cui collocare la barriera di ricarica, anche in condizioni idro-
geologiche complesse, come dimostra la letteratura scienti¿ca; per
questo motivo crediamo che la ricarica differenziale possa essere
effettuata senza dif¿coltà notevoli (Figura 5).
BIBLIOGRAFIA
B. N. Delaunay, “Sur la Sphère Vide”,
Bull. Acad. Science Ussr VII:
Class. Sci. Math.,
1934, 793.
H.J.Diersch, “FeÀow: Finite Element Subsurface Flow & Transport
Simulation System: Reference manual”, Wasy, Institute for Water Re-
sources Planning and System Research Ltd., Berlin, Germany, 2002.
S. J. Owen aand Ansys Inc, “A Survey of Unstructured Mesh Gen-
eration Technology, Dept. Civil and Environ. Eng.”, Carnegie Mellon
Univ., Pittsburgh, PA. [Online] Tech. Rep., 1998,
M. Vitali, “Hydrogeological study for the qualitative improvement of
groundwater”, Master thesis, Diiar, Politecnico di Milano, Milan, Italy,
2008.


